直线多次相遇问题是资料分析中的重要考点,这一类的题目其实难度不大,但是很多考生由于这一类问题比较抽象,理解不到位,产生了难度很大的错觉。因此,本文将重点放在如何让考生更好地理解何为多次相遇,以及如何解决此类问题的解题方法上。
与其他数量关系的题目一样,我们只要立好这一类问题的模型,找出其中的关系式,在日后遇到同类题目直接套用找好的公式即可,下面让我们来看一下,多次相遇追击的问题我们如何理解。
直线多次相遇,顾名思义,就是在一次相遇追击的基础上,两个主体继续运动——一般是直线的往返或环形的绕圈——以形成多次的相遇。那我们先来回顾一次相遇追击的公式,在直线的情况下,一次相遇公式为两个主体的速度和乘以时间等于两人的距离和,即总距离,用公式表示为:
![]()
也就是说,考查相遇问题的关键,在于他们的路程和,由此出发,我们开始考查直线上的多次相遇问题。
我们先来考查两端出发的相遇问题。假设甲乙两人同时从一条路的两个端点AB同时相向而行,速度为,第一次在路上某一处C点相遇了,然后他们不做停留继续前进,各自到达端点即时掉头,第二次在某一点D处相遇了,如下图:
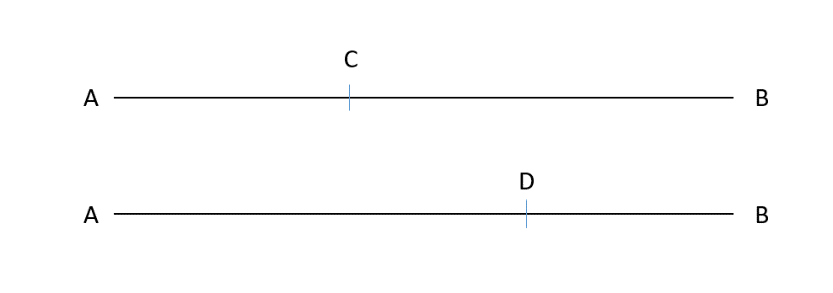
我们发现,甲走过的总距离为,乙走过的总距离为,而且,换言之,甲乙两人走过的总路程为,推广一下,我们可以得到两端出发的直线上多次相遇的公式:
![]()
如果他们同时从A点出发呢?甲速度更快,到达B点后掉头,在C点与乙相遇,如下图:
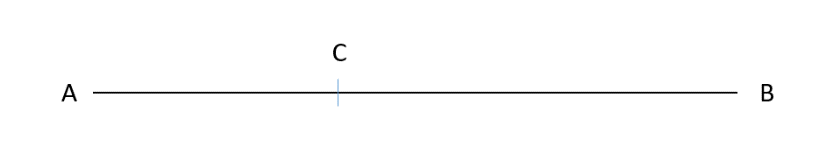
我们仍然从路程和的角度出发,此时甲乙两人走过的总路程为,推广一下,我们可以得到一端出发的直线上多次相遇的公式:
![]()
下面我们来看例题:
例(2021年广东省公务员录用考试《行测》)
小王和小李沿着绿道往返运动,绿道总长度为3公里。小王每小时走2公里;小李每小时跑4公里。如果两人同时从绿道的一端出发,则当两人第7次相遇时,距离出发点( )公里。
A.0
B.1
C.1.5
D.2
我们判断好这题是一端出发的直线上多次相遇问题,直接套用公式,代入数据,有2×7×3=(2+4)t,解得t=7(小时)。相遇时,小王走的路程为7×2=14(公里),14÷3=4……2(公里),距离出发点2公里。因此,选择D选项。
笔者相信,只要考生们理解了直线上多次相遇问题的本质,通过路程和来理解相遇问题,这一类题目就可以迎刃而解。













 点击刷新
点击刷新











