2024年国考行测数量关系备考:方程思想
一、考情分析
近年来公考大军越来越壮大,竞争更加激烈,想要脱颖而出,有一个好的笔试成绩就至关重要,充分的备考必不可少。当然备考也要讲究策略,在行测考试中,数量关系模块是一个锦上添花的模块,想要在短时间内又快又准的选出正确答案,就需要转换做题的思维方式,用最短的时间找出正确选项。数量关系考试中最常用做题方法要数方程法与代入排除法,以及其他的做题方法,这里我们探究一下方程思想。
二、基础概念

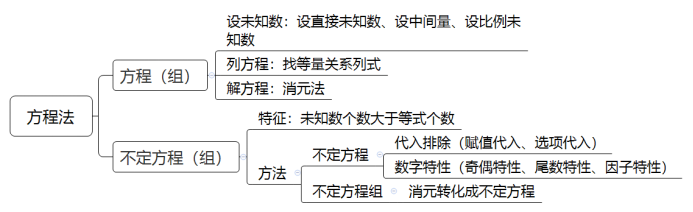
方程,其定义为含有未知数的等式称为方程。公考中常考题型又分为定方程(组)与不定方程(组),两种题型最明显的区别为:是否有唯一的解。而不论那种题型解题过程一样的,均为找等量关系、设未知数、解方程,其中核心步骤为找等量关系。
做题过程中,如何快速的得出答案不仅要快速的找到的等量关系,还要巧设未知数以便能够方便计算快速解方程。设未知数有哪些技巧呢,通过例题来探究一下吧。
三、常见题型
3.1、求什么设什么
例1、给贫困学校送一批图书,如果每个学校送80本书,则多出了340本;如果每个学校送90本书,则少60本。问有多少个学校?
A.30 B.40
C.50D.60
解,题中出现如果……如果……,存在明显的等量关系,且均与学校有关,设有学校x个,根据题意80x+340=90x-60,解得x=40,即有40个学校,故选B项。观察发现本题直接设所求项为x,列式求解即可求解。
3.2、设中间量
例2、给贫困学校送一批图书,如果每个学校送80本书,则多出了340本;如果每个学校送90本书,则少60本。问这批书一共有多少本?
A.3680 B.3760
C.3460 D.3540
解,观察发现与例1仅有问法不同,如直接设图书数量为未知数,需要根据学校数量相等列式,计算复杂,为了计算方便,设中间量学校的个数为x,则图书总数=80x+340=90x-60,解得x=40,则图书总数为90×40-60=3540。故选D项。观察发现直接设所求项不方便计算,考虑设中间量为x,列式进而求解。
3.3、设份数
例3、某有色金属公司四种主要有色金属总产量的1/5为铝,1/3为铜,镍的产量是铜和铝产量之和的1/4,而铅的产量比铝多600吨。问该公司镍的产量为多少吨?( )
A.600 B.800
C.1000 D.1200
解,观察发现题中有明显的等量关系,有因有多个份数,设有色金属总产量为15x,则铝为3x,铜为5x,镍的产量是铜和铝产量之和的1/4,则镍为2x,铅为15x-3x-5x-2x=5x,铅的产量比铝多600吨,则5x-3x=2x=600,即镍的产量为600,故选A项。观察发现题中出现多个分数,为了方便计算,避免等式中出现分数直接设总产量为nx份,即设份数,当题中出现分数,百分数,比例等时均可考虑设份数,以方便计算。
当然,除以上常用小技巧外,如果遇到需要设多个未知数,为了方便计算我们应该尽量减少未知数的个数,通过未知数之间的关系,由一个未知数表示另一个未知数以减少未知数的个数,方便计算。
四、小结
以上是在行测考试中数量关系模块中最常用的解题方法之一方程法中关于方程的运用小技巧,通过以上几种设未知数的技巧,在快速找到等量关系后,巧设未知数,方便计算以便于在短时间内找到正确选项。













 点击刷新
点击刷新











